Models are a statement in precise mathematical terms of an hypothesis about the way a system functions. The hypothesis can be tested, or validated, by comparing model predictions against observations in the field under the same set of conditions as those specified in the model. Validation of the model under a range of conditions increases confidence that the hypothesised mechanisms described in the model are correct. The validation procedure is not proof of a causal relationship, i.e. that the mechanisms in the model are the same as those in nature, but as its predictions are corroborated under differing circumstances, it becomes more and more probable that we have understood the system through our model. A very powerful approach is to use modelling in conjunction with experimentation. The model provides a machine for hypothesis generation, and a framework for hypothesis testing, that allows the experimental work to be logically structured.

It has been said that a model should be as simple as possible, but not too simple. We can start with something simple and refine it or make it more complex as evidence of its inadequacies become apparent. A model may be a complex mathematical structure requiring a computer to run it, or as little as a set of related regression curves, or even simply a set of verbal rules which lead to a range of predictions. It is never too soon to formalise what we know, or what we think we know. A model can be used to predict the likely impact of biological control agents and other control measures on the weed population under various scenarios. By rapidly testing a wide range of scenarios or hypotheses about the way in which the weed population and biological control agents could interact, the critical aspects of these interactions that are likely to determine the success or failure of the project can be identified for field testing and observation.

A number of general models for different types of plant populations have been developed; for example the Watkinson model for annual plants (Watkinson 1980), and the Leslie matrix models (Begon and Mortimer 1986; Leslie 1945) for plants with age specific fecundity and mortality (i.e. perennials). These basic models can serve as a starting point for development of a model for a particular species (e.g. See Watkinson et al. 1989; Hoffmann 1990 and Lonsdale et al. 1995).

Knowledge of the biology of the biological control agent and how control agents impact on the weed is required; the better the knowledge of the demographics of the weed the better the model. Such information can be gathered during initial laboratory and field testing in the country of collection, and in laboratory studies while the potential agent is being assessed for suitability to release. It may be necessary to undertake small-scale experiments in the laboratory or in the field after initial release of the agent to obtain the information required.

Advantages of the use of modelling are that it can:

Disadvantages of the use of modelling are that it:

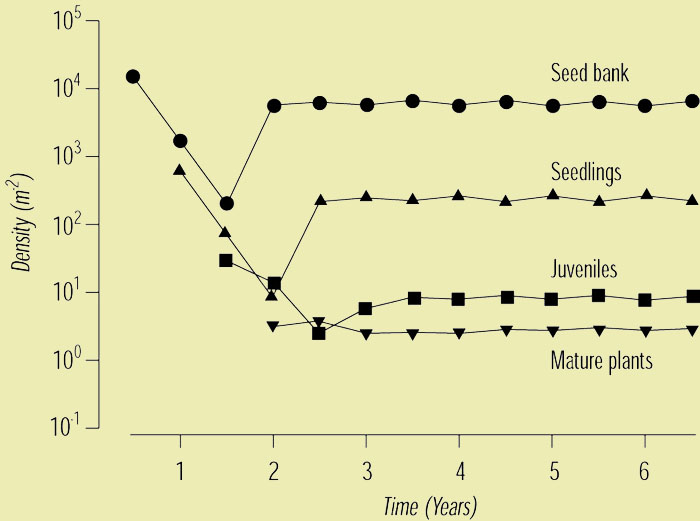
A matrix model that incorporates density-dependent fecundity, survival and growth has been developed for Mimosa pigra (M. Lonsdale and G. S. Farrell unpublished data). The model has been used to predict what happens to M. pigra, a weed with a large seed bank, when canopy plants are killed but the seed bank is left untouched. Mimosa pigra has a seed bank in the order of 10 000 seeds/m² and adult stand densities around 1 plant/m². The Figure below shows the result of model simulation of canopy removal, but with no impact on the seed bank. The role the seed bank plays in the weediness of this plant is apparent. Within two years a dense thicket has redeveloped and equilibrium has been reached within 4-5 years.

What happens if reductions to seed output are also modelled? An order of magnitude change to seed production reduces the seed bank, but only by a third. Reductions of seed output to one thousandth of the normal amount results in extinction. But with reduction even down to 0.003 of the normal output, mature stand density is still within the range seen in normal thickets and there is enough plasticity in plant growth form for mature plants to maintain a closed thicket down to around 0.1 plants/m². Massive reductions in seed output are required to impact on the weed.

Recovery of a Mimosa pigra population after a major disturbance has killed the mature stand (year = 0). At first, the seed bank becomes depleted as seeds germinate, but a proportion of these survive through the seedling stage to produce seeds as juveniles and adults. Within 2-3 years, a closed stand has returned.

[ Back ] [ Next ]